「數感盃青少年寫作競賽」提供國中、高中職學生在培養數學素養後，一個絕佳的發揮舞台。本競賽鼓勵學生跨領域學習，運用數學知識，培養及展現邏輯思考與文字撰寫的能力，盼提升臺灣青少年科普寫作的風氣以及對數學的興趣。
本文為 2019數感盃青少年寫作競賽 / 高中職組專題報導類佳作 之作品，為盡量完整呈現學生之作品樣貌，本文除首圖及標點符號、錯字之外並未進行其他大幅度編修。
- 作者：張原嘉、劉羿賢／新竹市立新竹高中
長城上的烽火台。圖/ flickr
前情提要
歷史上曾有一位絕世美人褒姒，她不愛笑，但她的美貌卻讓當時的天子周幽王神魂顛倒。周幽王為了取悅褒姒，在天下太平時三番五次點燃危急時召集 諸侯的烽火，當諸侯們匆忙趕來首都保衛天子時卻沒看到敵人，只見褒姒的訕 笑。西元前 771 年，犬戎入侵，失信於諸侯的周幽王，在真正危難時雖點燃烽火，卻不得諸侯信任，最終為犬戎所擄，只能含淚與褒姒生死相別。
歷史總是有無限的可能性，倘若那時有一位諸侯查覺到異狀，聯合全部諸 侯及時抵擋犬戎入侵，西周將延續國祚，而周幽王的名聲在後代終將大大改 變。 「各位臣子們，寡人對大家感激不盡，這是寡人的不對，寡人不應該隨便戲弄你們。」 此時權位最大的諸侯講話了，「王啊，所謂紅顏禍水，我們聯合要求您必須將褒姒賜死，否則何以面對被戲弄而失去軍心的軍隊呢?」
「這…寡人實在為難…」
「王，若您不將這妖女賜死，我們將另立新王，而褒姒將陪您在黃泉相見。」
周幽王噙著淚水，一條白綾，結束了絕世美人多舛的一生。
「吾王英明。」周幽王聽著眾臣高聲地朝拜，逐漸對褒姒之死釋懷，他想成為一位賢君，在歷史長河上留名，首要之務即是鞏固國防。正所謂「從何處跌倒，就要從何處爬起」，周幽王認為國家的烽火台制度亟需改善，因此，他徵求天下數學第一高手前來設計一套完善的烽火台制度，一次劃時代的改革將在數學中開展。
正文
周幽王向臣子展現強國的決心，貼出告示徵求烽火台的排列方式，只要設 計被認可即賞金千兩並加官奉爵。所謂重賞下必有勇夫，不到一天時間，全周 國數學最好的大臣便前來獻策。
「微臣對烽火排列略有涉獵，向王獻醜，請王指教。」
「愛卿別這樣說，寡人對您的建議十分有興趣，請說。」
「微臣稍加統計，周朝不含沿海地帶的邊界長度大約13000公里（註一），若照以 往以10里（等同於18公里）（註二）設置一個烽火台，那麼共約需 13000÷ 18 ≅722 座烽火台，便可占滿整個邊界。而周朝可派駐至邊界的軍隊共有 45000人（註 三），因此微臣建議在邊界每一烽火台配置 60 位士兵，當有蠻夷入侵時便點燃烽 火，使士兵集合到作戰地點，如此一來便可形成一道有效的防線，王您意下如 何?」
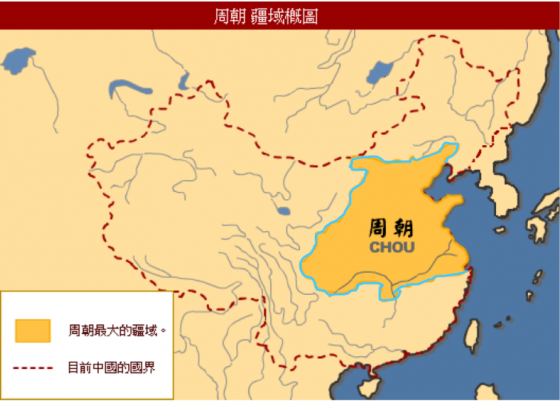
圖一／每日頭條。註：藍色部分為設置烽火台邊界（不含沿海部分）約為800 公里
周幽王聽大臣如此說明，臉上露出猶疑的神情，似乎對大臣的敘述不以為 然，說道:「好是好，那我怎麼知道這種防禦可以集結多少士兵，畢竟蠻夷行軍 的速度可達一天70公里（註四），而我國首都鎬京（今西安）距離邊界最短700公 里，代表蠻夷入侵至首都最快只要10天。我必須知道直線型排列烽火台間的平均距離，進一步推算出傳遞時間，才能知道有多少士兵會及時趕來。」
周幽王的問題：大臣設計的烽火台平均從一座烽火台傳遞至另一座烽火台平均傳遞時間？這是否能及時通報軍隊抵擋蠻夷？
「臣對此稍加研究，烽火一時約行百里（註五），代表每座烽火台之間的傳遞只要 6 分鐘。為了討論 722 個烽火台之間從一座烽火台傳至另一座烽火台所需時 間，我們定義總路徑長度 Ln 為 n 個烽火台中任兩個烽火台之間傳遞次數的總和，舉最簡單的例子，L2 = 1，L3 = 4，L4 = 10 （見圖二）。」
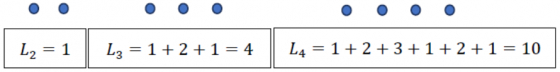
圖二
「寡人看出規律了，每一個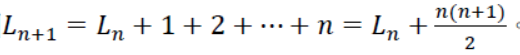 
」
「吾王英明，在點數為 n 的直線排列中，當增加第 n + 1 個點時，總路徑長度可看成原本 n 個點的總路徑長度加上新增加第 n + 1 個點到原本 n 個點的路徑長度，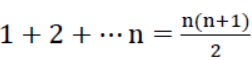
。在數列中我們將前項和後項的關係稱為遞迴，在 Ln 數列中，遞迴式為
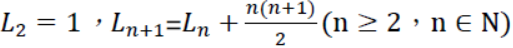，且由這遞迴式，即可求出 Ln 的通式解。」
「首先必須先把遞迴式寫出來，如下：
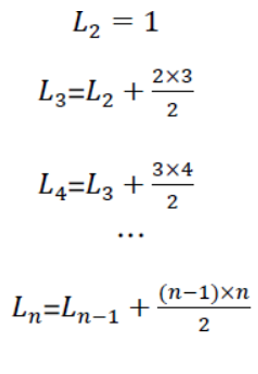
接著把上述式子全部相加，可發現 L2、L3…Ln−1 全部被消掉，只剩下 Ln 和 一堆數字，如下式。
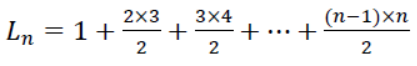
「到這裡我懂，但要如何化簡右式後面一連串的數字呢？」
「稟告王，在數學中求和有很多方法，最常用的方法為 Σ法，意思是將雜亂的代 數和化成許多連續正整數的n次方和相加。這招可計算出許多遞迴解的通式，但 缺點為太過雜亂，因此微臣推薦另一種計算通式的方法，分項對消。您是否有發現，在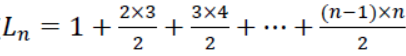
中，首項的 1 可先化成 1×2/2 ，若將分母的 2 先全部提出，可得 Ln = ½（1 × 2 + 2 × 3 + 3 × 4 + ⋯+ （n − 1） × n），其中級數中的每一項乘積都滿足前項和後項的頭尾相連。」
「愛卿所言甚是，這很像文字接龍，每一項乘積的前數都必須與他的前一項的後數相同。但是如何整理？」
「王先別急，我們先將每一項同乘以3，並將⅓提出，使得Ln = ⅙（1 × 2 × 3 + 2 × 3 × 3 + 3 × 4 × 3 + ⋯+ （n − 1） × n × 3）再來利用分配律的性質，
1 × 2 × 3 = 1 × 2 × （3 − 0） = 1 × 2 × 3 − 1 × 2 × 0，
2 × 3 × 3 = 2 × 3 × （4 − 1） = 2 × 3 × 4 − 2 × 3 × 1，
3 × 4 × 3 = 3 × 4 × （5 − 2） = 3 × 4 × 5 − 3 × 4 × 2，
…
（n − 1） × n × 3 = （n − 1） × n × （n + 1） − （n − 1） × n × （n − 2）。
因此Ln =⅙ [（1 × 2 × 3 − 1 × 2 × 0） + （2 × 3 × 4 − 2 × 3 × 1） + （3 × 4 × 5 −3 × 4 × 2） + ⋯+ （n − 1） × n × （n + 1） − （n − 1） × n × （n − 2）]」
周幽王臉色凝重的臉色在一瞬間豁然開朗，說道：「原來！如此操作之下前項的 1 × 2 × 3 即可與後項的 2 × 3 × 1 對消，而 2 × 3 × 4 可與 3 × 4 × 2 對消，直到最後只剩下（n − 1） × n × （n + 1）和首項的 1 × 2 × 0，因此
。」
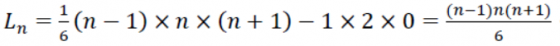「吾王英明，這就是分項對消的威力。若將實際情況代入，我國有 722 座烽火台，總傳遞路徑長度
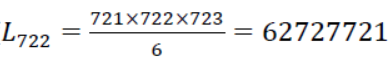
，而平均傳遞路徑長度為總路徑長度除以總路徑數，若有 722 座烽火台，每兩座有一條路徑，722 座烽火台 有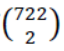 
= 260281 條路徑，故平均傳遞路徑長度= 62727721 ÷ 260281 = 241 條。」
「稍待一會，這平均傳遞路徑長度是否也有通式。前面算過當有n座烽火台時總傳遞路徑長度為
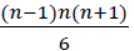
，其中有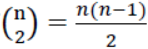
，因此平均傳遞路徑長度為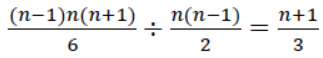 
。」
「王您實在有數學慧根，竟能直接求出平均傳遞路徑長度的通式，微臣自嘆弗如。」 看著周幽王臉上得意的笑，大臣心上的石頭放了下來，並接著說道：「若以兩座烽火台的傳遞為 6 分鐘來計算，當烽火台的士兵一發現蠻夷入侵， 平均只要花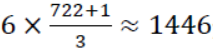
分鐘，即平均大約 1 天的時間便可以從任一烽火台 傳至另一烽火台，而蠻夷若想直接攻入首都需花 10 天的時間。因此倘若蠻夷再 入侵，我們可以先讓附近軍隊抵擋，拖延蠻夷入侵速度，再集結所有軍隊對付 蠻夷，相信我吾國必能永保太平，再無蠻夷攻入首都這檔憾事發生。」
「愛卿實在為朝廷之棟樑，國家之人才，能設計出有效的烽火台制度，並用遞迴原理佐證烽火台的傳遞速度足夠抵擋蠻夷入侵，你要什麼，美人、封地、還是爵位，朕通通給你。」
「報告王，這乃是微臣應當做的事，微臣只希望領取微薄俸祿，潛心研究數學，如此而已。」
「愛卿太過客氣，既然你教會我遞迴原理，我封你為遞迴大學士，並每天教導國人數學，讓數學應用在生活中，讓周朝再次因數學而富強！」
結語
「哈哈！那蠻夷一定不知我大周國有如此優秀的數理人才！」
「吾王萬歲！」在接受眾臣朝拜後，周幽王臉上盡是風光滿面的神氣。一階階 爬上烽火台的高台，此時的周幽王卻歛起笑容，若有所思地望著遠方，心中升 起一股淡淡的哀傷，「倘若褒姒還在，我可以教她有趣的數學，那她將以崇拜的 眼神投向我，那我會是多麼幸福！唉！我用最艱深的遞迴方程式也計算不了褒姒一抹淺淺的微笑，最複雜的通式解也比不上我對褒姒無盡的思念。」
地平線上連著一座又一座的烽火台，一片祥和的風景中，周幽王看見褒姒翩翩的身影如烽火一般冉冉上昇，一抹淺淺的微笑從遙遠的烽火台上，傳至更遙遠的烽火台。
相關連結
- 高中數學第二冊第一章──數列與級數
- 高中歷史第二冊第一章──商至西周的文明發展
參考資料
- 註一 每日頭條:周朝疆域範圍:「分封制」西周分封諸侯圖
- 註二 中文百科在線:烽火台
- 註三 百度百科:西周
- 註四 每日頭條:古代騎兵行軍速度到底有多快?讓你想不到堪比現代裝甲部隊
- 註五 良工的博客:古代烽燧，軍情的傳遞速度有多快?
更多2019數感盃青少年寫作競賽內容，歡迎參考 2019數感盃特輯、數感實驗室官網及粉絲頁喔。
The post 《周幽王的烽火台──探討烽火台平均距離的期望值》——2019數感盃 / 高中職組專題報導類佳作 appeared first on PanSci 泛科學.