- 【科科愛看書】一直以來人們都渴望飛翔的滋味，但是，難道發明了飛機就能讓大家隨心所欲亂亂飛嗎？密如蜘蛛網的全球航線究竟是如何設計的？那麼多的飛機要怎樣才不會撞在一起？為什麼起降時要特別小心翼翼？快來一窺《飛航管制的祕密世界》，讓你知道空中飛人背後的團隊有多厲害！
用數學來創造航空交通的模型吧！
本文將簡單介紹我進行的 TOPAZ 相關工作。例如，導入 ASAS 之類的新航行模式的未來航空交通流，該如何在電腦中進行模擬呢？讓現實中的系統得以虛擬化，在電腦中模擬重現交通流的作業，稱為「創造模型」。TOPAZ 就是應用數學手法，創造出未來航空交通的模型。
TOPAZ 使用的數學模型源自德國學者卡爾．亞當．佩特里（Carl Adam Petri）在 1960 年代提出的理論計算模型「佩特里網」（Petri net）。佩特里網用以記述並分析資訊的流動和控制，適用於複數個事件並行、非同步發生的系統。它可檢驗「狀態變遷」（state transition）的情況，所以適合用於模擬。此外，佩特里網可表現出並行性、非同步性，具有可驗證系統整合性、容易找出變更下的影響範圍等優點，在飛航管制科學領域是極好用的計算模型。
要利用電腦模擬空中交通流的情形，數學必不可少。圖／By Wallpoper , Public Domain, wikimedia commons
利用計算模型，咖啡也能喝得很科學！
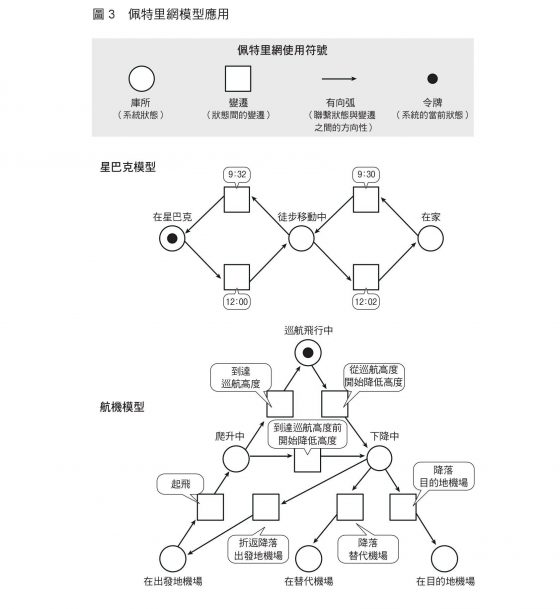
佩特里網模型的系統可用「○」、「□」、「→」、「●」四種符號來表現：
- ○（庫所〔 place 〕）表示系統狀態
- □（變遷〔 transition 〕）表示狀態間的變遷（顯示變遷時的條件）
- →（有向弧〔 arc 〕）表示聯繫狀態與變遷之間的方向性
- ●（令牌〔 token 〕）表示系統的當前狀態
或許大家腦海中還是無法形成整體概念。但我必須說這是相當優異的模型，甚至可將我們的日常生活整理成模型來表現。下面舉例說明：
假設「我」正在離家最近的星巴克寫作。由於今天是週六，我在比平日稍晚的九點起床，帶著筆電走到星巴克。抵達後，邊吃早餐邊喝咖啡歐蕾，開始敲打文字。我計畫先努力寫到十二點，再暫時回家午睡。我在正午前的這些活動，可以用簡單的佩特里網模型表現如下方圖 3。
用佩特里模型喝杯科學的咖啡吧。圖／《飛航管制的祕密世界》
首先，將我的狀態分成「在家」、「徒步移動中」、「在星巴克」三個選項。在這個假設中，各項活動會因時間不同而產生變化，因而設定時間為變遷條件。早上九點起床，九點三十分離開家，步行兩分鐘後抵達星巴克，也就是說從「在家」變遷到「徒步移動中」狀態，是基於「時間九點三十分」的條件。
同理，狀態從「徒步移動中」變遷到「在星巴克」，於「時間九點三十二分」的條件下成立。反向變遷亦然，條件「時間十二點」促使狀態從「在星巴克」變遷到「徒步移動中」；條件「時間十二點二分」，狀態從「徒步移動中」變遷到「在家」。我目前「在星巴克」，當前狀態（token）處於「在星巴克」的系統狀態（place）。
化繁為簡，航空交通不困難
接下來利用相同邏輯，試著設計簡單的航空交通模型。
首先試想從「出發地機場」起飛直到降落「目的地機場」的航機模型。將航機狀態設定為「在出發地機場」、「爬升中」、「巡航飛行中」、「下降中」、「在目的地機場」或「在替代機場」等六種情況。因為天候不佳等因素無法降落目的地機場時，飛機將降落於事先決定好的替代機場；或者，有時因飛行中發生緊急狀況，無法降落目的地機場，可能折返出發地機場或降落替代機場。
考量上述六種系統狀態的變遷，假設共有七種狀況，個別給定如圖 3 所示的變遷條件（下方圖 4 的航機模型亦同）。
在這個模型中，需要考慮的是一旦發生緊急狀況，航機該折返出發地機場或降落替代機場。
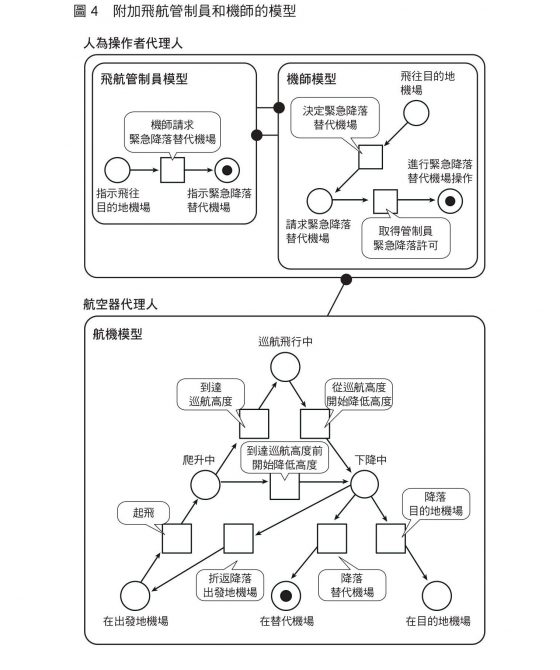
因為對機師做出允許變更飛行路徑指示的是管制員，為了讓飛機順利降落，必須思考下列兩者如何動作，一是管制員，一是與管制員通訊後在駕駛艙輸入飛行指令的機師。這些互動過程可以統整成如圖 4。繪製出管制員與機師各自的簡易模型，再附加在航機模型上。
附加飛航管制員和機師的模型。圖／《飛航管制的祕密世界》
接下來我們先做出管制員與機師的簡易模型，再試著連結航機模型，聯繫三者的線段稱為「有向弧」，表示聯繫的兩端之間有資訊流通，且資訊是來自繪有黑點的模型。
為了簡化模型，將管制員的狀態設定為「指示飛往目的地機場」和「指示緊急降落替代機場」兩種；機師的狀態則有「飛往目的地機場」、「請求緊急降落替代機場」、「進行緊急降落替代機場操作」三種選擇。
管制員模型從「指示飛往目的地機場」變遷到「指示緊急降落替代機場」的條件設定為「機師請求緊急降落替代機場」。管制員狀態呈現「指示緊急降落替代機場」時，機師模型的當前狀態會變遷為「進行緊急降落替代機場操作」。
有了模型，不怕航班亂成打結的蜘蛛網
運用佩特里網即可表現出管制員與機師間的相互影響，兩者互動所產生的決定反映為航機的狀態。航機在ASAS下自主飛行等情況，可將機師與飛航管制員視為同一「人為操作者」（human-operator）團體（即代理人〔agent〕）。模擬複數代理人相互影響的狀態的模型，稱為「多代理人模型」（multi-agent model）。
透過前述做法，可在 TOPAZ 中將未來的航空交通編寫成數學模型。真實系統的模型比前面介紹的更繁複，因此佩特里網在模擬系統的相互影響上就更加便利了。
全球航線無比複雜，需要模擬模型才能讓空中交通更為順利。圖／By Martin Grandjean, CC-BY-SA
佩特里網的最大優點是，可以將長篇大論的文字說明化為一張圖示；只要再將個別狀態的變遷條件記錄在說明手冊上，參與計畫的所有成員就可共享資訊。
也就是說，捨棄文字說明這類容易招致誤解的表現方式，依事先訂定的規則記錄模型。再者，還可組合各類數值，如航機高度這類連續變化的值、飛航管制員的判斷等離散變化的值，或機師和管制員的反應延遲、稀少事件發生等導入機率論來表現的值。福克公司的航空器模型也是運用佩特里網結合航空交通模型，模擬在交通流中的航機動態。
本文摘自《飛航管制的祕密世界：從地面到天空，從管制台到駕駛艙，飛航第一線直擊全紀錄》，臉譜出版。
The post 如何讓空中航班不打結？用數學來模擬一下吧！──《飛航管制的祕密世界》 appeared first on PanSci 泛科學.