快還要更快!學習物理的重點就是要「快速解題」?

不能只有快,還要更快?圖/giphy
在我的教學經驗中,有些學生會問我:「老師這一題有沒有更快的解法、一個式子就可以解出來?」我總是笑笑的說:「有,不過你還是要完全了解整個物理意義與過程,才能知道快速解法的來由,才能說出一番道理,才能有你自己的想法。」
我完全可以理解學生為什麼需要「快速的解法」,癥結還是:面對學校期中考或 未來的升學考試時,有答題時間限制的壓力。
一般學校期中考,物理科答題時間為 70 分鐘,考題大約 20 題到 25 題左右;升學考試自然科學測 68 題,答題時間 110 分鐘;指定考科物理科答題時間 80 分鐘,回答 26 題到 30 題左右,題數多寡由命題老師依據題目難易度來酌量。因為答題時間有限制,為了能拿到高分數,學生自然希望每一單元都能有快速解題法。

學習過程畢竟不是只為了考試,升學考試只是其中一個目標。圖/Pixabay
然而,學習過程畢竟不是只為了考試,升學考試只是其中一個目標,高中的學科基礎,會影響大學的學習成效,學習物理還是要建立蓋房子的鷹架模式——九層之台,起於累土;合抱之木,生於毫末;千里之行,始於足下。學習物理還是要「盈科後進」,不宜囫圇吞棗,避免「繁枝容易紛紛落」的速成之弊,才能體會學習物理時「嫩蕊商量細細開」的自然生發之美。
有一則幽默小品文:
聯合國給全世界的小朋友出了一道題目:「對於其他國家糧食短缺的問題,請您談一談自己的看法。」非洲的小朋友看完題目後,不知道什麼叫「糧食」;拉丁美洲的小朋友不知道什麼叫「請」;歐洲的小朋友不知道什麼叫「短缺」;美國的小朋友不知道什麼叫「其他國家」;台灣的小朋友不知道什麼叫「自己的看法」。
雖然只是一則網路幽默文章,可是台灣學生努力符合標準答案,戮力要得知快速解法,恐怕是不爭的事實。我鼓勵大家在學習時,多思考、多質疑,或許就有更多人能超越標準答案和快速解法,提出創造性的看法。
所以說,解題最重要的核心到底是什麼?
有句話說:「得魚忘筌」,「教材課本」是這個「筌」,而「思考能力」是那個「魚」。我期盼同學們學習物理時,能完全了解整個物理單元和例題習題的思考過程,不必急著要公式和快速解題方法,因為完整的物理概念才能讓我們具備帶得走的能力。
我舉個物理運動學的題目來說明:
有一飛行物體以速度 19.6 公尺/秒等速度上升,在離地面 24.5 公尺高空處掉落一個包裹,忽略空氣阻力的影響,且該處重力加速度 9.8 公尺/秒2,回答下列的問題:
- 此包裹上升的最大高度約為多少公尺?
- 離開飛行器至落地的時間有多久?
請你先仔細閱讀題目並且了解問題在問什麼之後,再看以下的解釋。
第 1 小題
分析:以包裹離開飛行物體的位置為坐標原點,建立一鉛直的坐標系統,方向以向上為正,向下為負。
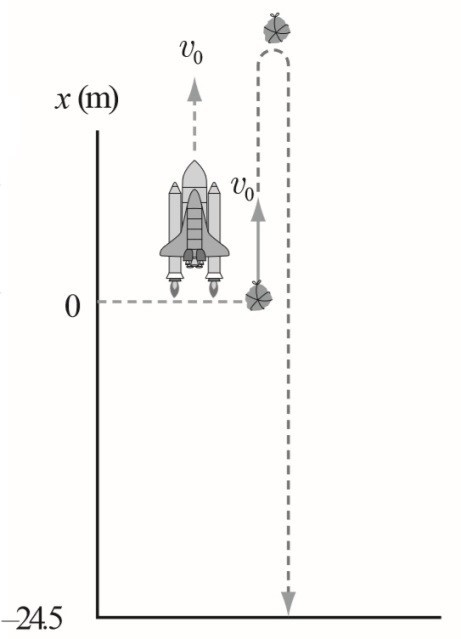
包裹離開飛行器示意圖。
此包裹離開飛行器時,為初速度 19.6 m/s 的鉛直上拋運動,此包裹上升至最高點時的速度量值為 0 。求解:如圖,包裹由出發點上升至最高點的位移 h 表示如下:
\begin{equation}0 = (19.6)^{2}-2\times 9.8\times h \rightarrow h=19.6(m)\end{equation}
所以,包裹離地的最大高度 H 為:
\begin{equation}H = 24.5 + 19.6 = 44.1 (m)\end{equation}
第 2 小題
- 第一種解法:
此包裹由釋放至最高點的時間 \(t_{1}=\frac{19.6}{9.8}=2(s)\)
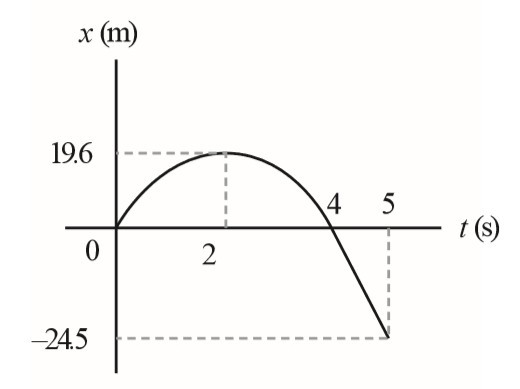
包裹的高度與時間關係圖。
由最高點落至出發點的時間 \(t_{2}=t_{1}=2(s)\),最後由出發點落至地面的時間\(t_{3}\)為\(-24.5=-19.6t_{3}-\frac{1}{2}\times 9.8t_{3}^2\)\((t_{3}+5)(t_{3}-1)=0\rightarrow t_{3}=-5\)(不合)或 \(t_{3}=1(s)\)
所以由出發至落地的時間為\(t_{1}、t_{2}、t_{3}\) 的總和為 5 秒。
- 第二種解法,為符合物理概念的快速解法:
此包裹由出發至落地的位移,根據所訂定的坐標系統為 −24.5 m,包裹從出發至落地的時間 t 示如下:
\((t-5)(t+1)=0\rightarrow t=5\) 或 \(t =-1\)(不合)
所以,包裹由出發至落地的時間為 5 秒。
學習物理的運動學單元時,鉛直上拋是很重要的等加速運動的例子,這是因為(1)鉛直上拋的「速度」及「時間」這兩個物理量,都具有對稱的性質,以及(2)從最高點落地的過程為自由落體運動;因此,要能了解這當中的物理概念,充分利用這些性質,才可以簡化解題過程。

討論運動學時,誰是「觀察者」很重要。圖/pixabay
討論運動學時,有一重要概念需「常在我心」,那是「誰看誰的相對運動」,換句話說「誰是觀察者」很重要。這絕對無法透過背公式、快速解題就能得到答案。讀者不妨思考以下這題北一女期中考的題目:
忽略空氣阻力影響,重力加速度 g 為 10 公尺/秒2。雙十國慶日上午,一架直升機在高空以 50 公尺/秒 等速度沿直線水平飛行。機上搭載兩名傘兵甲和乙,準備在廣場上空表演特技。對飛機而言,甲先從機上靜止落下, 2 秒後乙接著也靜止落下,但兩者的傘具皆暫時不張開,而在空中自由下降。回答下列問題:
- 甲跳落 5 秒後,甲與乙之間相距多少公尺?
- 當乙剛跳落時,甲利用一彈射裝置將一小球相對於甲以初速度量值 24 公尺/秒對準乙射出,則經過多少秒後,乙可以接到小球?
說明:
這是運動學的相對運動問題,對地面或地球而言,傘兵甲和乙的水平速度等於飛機的水平航速 50 公尺/秒,因此當乙從機上跳落時,甲的位置正在其正下方處。
1.甲跳落 5 秒後,乙正好跳落 3 秒後,此時甲與乙相距 H。
H =(甲掉下來位移)−(乙掉下來位移),寫成\(H=\frac{1}{2}\times 10\times 5^2-\frac{1}{2}\times 3^2=80\)公尺。
2.當乙剛跳落時,甲與乙兩者對地面的加速度相同,也就是乙觀察甲並不是等加速運動,而是等速度運動,兩者的相對加速度是零。
此時甲對地面的速度垂直分量為\(V_{Y}=gt=10\times 2=20\)公尺 / 秒,甲乙相距\(Y=\frac{1}{2}\times 10\times 2^2=20\) 公尺。
從甲看乙,乙以 20 公尺 / 秒的相對速度垂直向上遠離甲,當小球相對於甲以初速度量值 24 公尺 / 秒對準乙射出,則小球對乙的相對速度為 \(24−20=4\) 公尺 / 秒等速向上接近乙,經過 \(\frac{20}{4}\) 秒後, 也就是 5 秒後,乙可以接到小球。
此時甲、乙兩人相距\(20\times 5+20=120\) 公尺。
「考得好差,我肯定不適合讀物理」這樣想就錯囉!
學習任何一科目難免會碰到瓶頸與困境,學習高中物理亦然。

絕對不要因為成績低就下結論說自己不是學物理的料,高中物理沒救,這樣思考太悲觀。圖/energepic@Pexels
初學物理的高中生常有刻板印象,認為物理科很困難,原因可能是受到學長姊的經驗談所影響,也可能是國中時期就產生的感受,或受到期中考題難度高、分數低的影響。
遇到物理成績低時,究竟該如何面對?我建議同學們學學白居易面對被貶時的心境轉變,偶遊大林寺,竟然有新的發現,找到心中的「桃花」。
你不妨想一想:物理成績低的原因是不是學習方法不正確?是不是沒有完全消化上課內容?我確實認真學習嗎?我把心思放在物理嗎?物理成績低的原因很多,但絕對不要因為成績低就下結論說自己不是學物理的料,高中物理沒救,這樣思考太悲觀。
自我探索、改變方式,再給物理和自己一次機會

到底該怎麼讀才好呢?圖/GIPHY
每一年都有學生問我:「老師,怎麼辦?我兩次物理期中考都不及格,我有能力學物理嗎?」「老師,我的物理成績這麼低,我還有救嗎?」聽完這些吶喊,我總耐心地告訴他們:「我們來分析你怎麼學習物理,給物理的時間足夠嗎?」「上課認真聽講嗎?整理筆記嗎?做了哪些基本功?」與學生互動後,幫這些心中有迷惑的學生找出路,鼓勵他們突破迷思,回到最基本的「實事求是」,並且確實能執行自己要改進的計畫。
經過自我探索,改變學習方式後,大部分的同學在期末考都能重新出發,找回學習物理的信心。當然,如果只停留在「半暝全頭路,天光沒半步」(台灣俗諺)的「坐而言,起不行」,成績就沒有起色。
物理成績低代表的應是「學習方法和態度有問題」,並不代表自己的腦袋不好。
想突破學習困境,還有一件事很重要:練習多思考,不要「人云亦云」。譬如學到摩擦力的時候,可以試著想一想:摩擦力是不是都是阻力?它的方向永遠與運動方向相反嗎?有沒有可能方向相同或垂直呢?
改變學習方法,學會深入思考、多思考,是學習的不二法門。千萬不要輕易因為物理成績低,就下定論自己能力差而學不好物理。

本文摘自《如何學好高中物理》,2019 年 7 月,天下文化出版。
The post 物理總考不好怎麼辦?一起從根本改變吧!──《如何學好高中物理》 appeared first on PanSci 泛科學.