- 作者/李政憲
對應:七年級「三視圖」、九年級「生活中的立體圖形」
需要道具:名片紙(長寬比例約 1.6:1,建議有 4 種顏色)、色紙
增加立體空間感的「三視圖」!
在十二年國教的 108 新課綱上路後,數學課中多了一個「三視圖」的概念,這個三視圖,不只能夠增進同學們的立體空間感,也和時下正夯的 3D 列印等新科技作結合。
什麼是三視圖呢?三視圖指的是將一個立體圖形,從前、後、左、右與上、下六個面,解構它從不同方向所看到的形狀,並以平面的方式呈現。以圖 1 為例,我們可以從六個方向看到不同的形狀,這也就是圖 2 中六個方向的「視圖」。
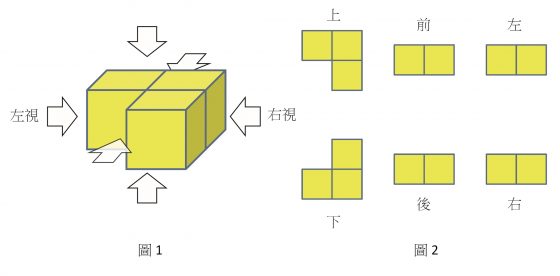
圖/臉譜出版提供
仔細觀察圖 2,你會發現上下兩個視圖是對稱的,而前、後與左、右視圖是相同的。難道所有的立體圖形的對向視圖不是對稱就是相同的嗎?另外,既然有六個面,為什麼叫做「三視圖」呢?這些疑惑,就讓我們用隨手可得的名片紙,實際做出一個圖 1 中的立體連方塊來觀察解惑吧!
用名片紙摺出立體連方塊!
- 要怎麼用名片紙做出立體連方塊呢?讓我們先從做出一個立體方塊開始吧。
請你拿起兩張符合一般名片紙比例的名片(一般的名片紙長寬比大約是 1.6:1 左右【註一】),將它們以上層直向、下層橫向的方式疊合出一個正方形(如圖 3)。

圖 3
李老師小聲說:「這個正方形同時也一定會是這個長方形中最大的正方形,為什麼呢?請自己思考看看後再看【註二】的答案。」
接下來,將直向的名片紙水平向右移動一些(如圖 4),使得重疊部分兩側多出來的部分寬度差不多,再將多出來的部分往上摺(如圖 5)。

圖 4

圖 5
接著翻面,將另一張名片沿垂直方向移動,同樣將兩側多餘的部分調整至等長,並往上摺製出一組互扣的正方形(如圖 6)。

圖 6
請用同樣的方法,再製作出共三組的互扣正方形(如圖 7)。

圖 7
- 接下來我們要將這六張正方形拼組為一個正方體。
首先將六張互扣的名片紙拆開,將其中一張放置桌面,並將另一張名片紙與第一張名片紙方向垂直擺放(如圖 8),再將第三張名片紙與這兩張名片紙互卡(如圖 9),至此請你確認每張名片紙兩側的長方形,是否都卡在另外兩張正方形的外側。

圖 8

圖 9
想像我們目前搭組的三張名片紙分屬一個正方體的下方、右方與後方三個面,接下來請將前方、左方與上方分別搭建一張名片紙 ,使得前後、左右與上下分別對稱,即可完成一個正方體(如圖 10)。記得同樣要注意每張名片紙兩側的長方形是否都卡在外側。【註三】

圖 10
由於我們要完成的是三個方塊的連接,所以接下來請各位再辛苦一點,繼續摺製兩個同樣的方塊如圖 11,摺好後就可以進行方塊的連接囉!

圖 11
- 要怎麼將兩個方塊連接起來呢?
首先,將兩個方塊以同樣方式擺放(如圖 12),接著將其中一顆旋轉九十度(如圖 13),再將兩個方塊多出來的長方形部份互扣,就完成兩個方塊的連接了(圖 14)。

圖 12

圖 13

圖 14
然後,用同樣的方式,我們可以將第三顆方塊與前兩個方塊的組合連接(如圖 15),於是我們不用膠水與膠帶,就完成了以三個方塊所組成的立體連方塊囉!
李老師小聲說:「如果有需要理解或複習對稱概念的讀者,可參考前一章〈摺紙數學初體驗──從鑲嵌摺紙談對稱的應用〉的內容。」

圖 15
- 但做好了連方塊之後,你可能會覺得這個作品有點鬆鬆的,容易散開。沒關係,讓我們再為它加工一下!
請準備三種不同顏色的名片紙,先以之前摺製正方體六個面的方式分別摺出六張、四張與四張(如圖 16),再將摺完的名片紙於三連方每個表面的外側和長方形扣接(如圖 17)。
李老師小聲說:「建議先從相連方塊的內側L型部份先作扣接,再逐步扣接外側,比較容易完成且美觀。」

圖 16

圖 17
在扣接時,可以讓上下兩面、左右兩側與前後兩側使用同一種顏色的名片紙,就正式完成這個三連方了(如圖 18)。你會發現成品加了外側名片紙後,明顯要比之前穩固許多。

圖 18
「三視圖」和對稱有什麼關係呢?
完成後的作品,我們不妨想想其與對稱性的關係:除了剛剛我們製作作品時,應用了對稱的原理以外,我們應用了三種顏色的名片紙做為其表面,也恰巧符合三視圖的概念:從上、下看的時候顏色相同,圖形對稱;左、右與前、後看的時候顏色相同外,圖形完全相同──想想看,全等不也是種對稱的概念應用嗎?

圖 19
由於這六個方向的視圖都是由正方形結構所組成,不是兩兩對稱就是兩兩全等,所以我們只需其中三個方向的視圖就能完整描述我們的作品,而其實多數由正立方體組成的立體圖形透過「正面、側面、上面」三個方向的視圖,就可以表示出它的形狀及尺寸,這也就是叫做「三」視圖的原因。
李老師小聲說:「若正立方體的數量較多或非正立方體所組成的立體圖形, 則前後的輪廓圖雖然相同, 中間的線條則未必會對稱。」
此外,我們內部用到的同色名片紙,所完成的是這個連方塊的體積部份,外部扣接的三色名片紙,所完成的恰是這個連方塊的表面積。
有了這些概念以後,我們還可以接著製作更多的連方塊當作積木來堆疊(如圖19),設計製作出更有趣的立體作品,不妨發揮自己的想像力玩玩看囉!
註解:
- 註一:有興趣進一步研究名片紙長寬比與其延伸概念的朋友不妨可以參考《科學教育月刊》345 期「摺紙中學數學」之〈名片試金石〉,中華民國 100 年 12 月號。
- 註二:重疊的部分是不是這個長方形裡最大的正方形呢?試想一下,如果這個正方形不是這個長方形中最大的正方形,則必存在一個邊長比這張名片紙的寬邊還長的正方形,若我們按著大於寬邊的長度繪製一個正方形如下圖,明顯可以觀察到這個正方形的一邊會超過原來名片紙的大小,所以兩張名片紙重疊的部分確定是這張名片紙裡面最大的正方形。
![]()
- 註三:此名片紙摺正立方體的摺法主要參考自網路,請各位讀者搜尋影片關鍵字「origami business card」即可找到相關的影片。

——本文摘自泛科學 2019 年 10 月選書《藝數摺學》,2019 年 9 月,臉譜出版。
The post 我把我對摺,輕輕把你也對摺~用名片紙摺出立方體! 還能談談三視圖與對稱──《藝數摺學》 appeared first on PanSci 泛科學.
