「國小數學不外乎加減乘除,能設計出什麼有趣的活動嗎?」
約莫兩年前,我開始規劃「動手做」的數學實驗課,請教幾位國中老師,他們建議我從國小著手,一方面國中課業壓力大,一方面國中生對數學的好惡相對定型,不如從小學做起。
開頭的那句話,就是我聽完建議後的第一反應。

國小數學不外乎加減乘除,有什麼有趣的地方?圖 / 石川内野手
當時我認為越深奧的數學,越能展現出有趣、特殊的應用,例如用微分方程表示男女的戀愛關係,用機率求找到理想情人的可能性。小學數學的基礎運算、多邊形、單位、時間、分數、小數,說得好聽點是「少數買菜會用上的數學」,但換個角度,好像還真只有買菜這類單調普通的生活應用。
兩年後回首,只覺得以前見識真淺。國小數學雖然簡單,卻是「大巧不工」,如同作者阿哈羅尼教授講起他重新走入小學的心得:
我學習到的很大一部分並非新的事實,而是全然不同的東西,也就是那些細微的層次。這有點像欣賞一片布料,遠觀好似平順均勻,但是拿到眼前就會察覺是由精細交織的線所構成︰我原先當成是一體的概念,卻是由精細的觀念編織出來的。
我對這段話感同深受。
相似概念的細微差異
舉個切身的例子,我以前覺得比就是兩個數字中間加個「:」,比值的另一種表示法。百分比、最簡單整數比大同小異,考試注意不要寫錯就好。
當我為了教小學生,強迫自己思考它們的差異時,才體會到原來,比是從生活中找到的2組數字,最簡單整數比是為了看出那些「比」相等,比值、百分比,引用本書說法是「比的共同語言」。
要比較比值,最簡單的例子就是看看現在到處都是的螢幕啦!圖/pexels
以電視螢幕為例,走進 3C 賣場,挑一台螢幕量它的長與寬,你會得到兩個數字,建立出一個比,以40吋螢幕來說,這個比約是34.9:19.6(吋,四捨五入到小數點下第一位),如果是50吋就是43.6:24.5。不同大小的螢幕有不同的比,看似不一樣,但當它們都化簡成最簡單整數比——16:9,你就知道所有螢幕的長寬比相同。
如果旁邊有一台傳統的4:3螢幕,你想知道哪種螢幕比較寬,就要進一步用比值:
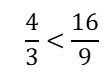
原來每一種「比」都有不一樣的意義與用途(我相信許多國小國中老師深知這點,在此請允許我野人獻曝一下)。然而,在(至少我)過去學習的歷程中,我們比較不常強調這個細微的差異,比較多著重在
「如何從比化簡成最簡單整數比,求比值、或表示成百分比。」
概念之間機械性的連結固然重要,卻不是唯一重要的事。
串聯理解不同的知識
本書的作者阿哈羅尼教授與譯者李國偉老師都是非常傑出的數學家,對數學的了解相當深刻,不僅釐清了小學許多相似數學概念的差異,還能跨越不同概念,解釋它們的共同之處。我對一段「單位與分數」的類比印象深刻:
3 根香蕉與 4 顆柳橙共多少?

柳橙和香蕉:「找我們?」(設計對白)圖/youtube
有些大人(包括老師)認為單位不同,無法相加。但若是退一步用「水果」這個單位涵蓋香蕉跟柳橙,把問題變成
3 個水果與 4 個水果共多少個水果?
答案無庸置疑是 7。再來看分數的加法
1/2 + 1/3
大家都清楚第一步是通分,找公分母。對照水果的例子,你會發現兩者有著一樣的邏輯。我們可以把分母看成一個「單位」,1/2 和 1/3 的分母不同,表示單位不一樣,通分相當於退一步,讓它們變成同樣的單位,就像前面用水果來取代香蕉跟柳橙。有了公分母 6,便能輕易完成加法
1/2 + 1/3 = 3/6 + 2/6 = 5/6
學數學不費力,反而省力
我很希望小學生能在數學課中感受到數學的秩序、推廣、以及簡潔表示法,作者將這三點命名為「數學的三種省力法」。多數人覺得學數學很吃力,事實上恰好相反,數學的一個目的是為了幫助我們省力。高斯發現 1 加到 100 這 100 個數字中,1+100=101,2+99=101,3+98=101,一共是 50 組 101,答案是 50×101=5050。

圖/pixabay
這就是秩序,或有時候稱作規律。不妨把這個問題想得更完整一點,今天一位攤販去果菜批發市場(你可以跟北農連結在一起,如果你覺得這樣會更時事一點),一個中盤商擺了 100 堆蘋果,第一堆有 1 個,第二堆有 2 個…依此類推,攤販想知道總共有幾個,評估是否要全部收購。根據攤販的數學程度,會發生以下三種狀況:
- 連加法都不會。只能將 100 堆蘋果看做 1 堆,扳著手指慢慢數。數 2 顆需要 1 秒,預計得花上 42 分鐘。
- 會加法,但無法觀察出兩項相加是 101 的規律,得一項項慢慢加,平均1次加法花 3 秒,他得用掉 4 分 57 秒。至少快了 8 倍多。
- 會加法,且能觀察秩序。50×101=5050,全程花不到 10 秒。比第一種快了約 250 倍。
這就是數學省時省力的威力,也是目前強調的數學素養的一個面向:不只會解題,還能找到有效率的解題方法。
如果學生能感受到數學的巧妙與用處後,相信會更願意學習數學,也更知道該如何運用數學,再更多地方尋找秩序建立方法、將建立的方法推廣到不同的應用、並且運用簡潔的表示法。書中還講了好幾種實用的教學技巧,例如:
- 用具體的例子傳達抽象概念
- 一節課應該經歷三階段:從具體出發,畫圖,最後走向抽象
- 不跳過精確的命名,清晰定義概念
- 概念必須通過學童親身經驗才能產生
讓你一讀完就能實踐。如果你反覆仔細閱讀好幾次,更能體會作者所說的:
小學數學雖然不深奧,但包含智慧;雖然不複雜,卻有深意。

小學數學雖然不深奧,但包含智慧;雖然不複雜,卻有深意。圖/wikimedia
很感謝李國偉老師引進、親自翻譯本書,讓大眾有機會從大師的角度,重新認識小學數學。也希望我們真能如老師在譯者序提到的(註):
開創書面作業以外的動手實作或身體活動,幫助學生體會出生活周遭處處可發現數學的蹤跡。
我深信,當一位小朋友走到哪裡,就像對他熟悉的玩具角色一樣,能看見生活周遭的數學蹤跡(螢幕長寬比、時間的六十進位制、買蛋糕時呎吋跟實際大小的關係),那他的數學一定不會差到哪裡去,不,應該是一定會很棒。
- 註:小小的預告,《小學算術教什麼,怎麼教》(天下文化)是給大人看的小學數學,馬上來臨的暑假,我與金鼎獎作家王文華老師將合作推出一套給小學生看的《數感小學冒險》系列(親子天下),也敬請期待噢。
The post 國小數學哪有那麼容易?雖不複雜,卻有大巧不工的深意──《小學算術教什麼,怎麼教》推薦序 appeared first on PanSci 泛科學.