2018年9月24日,台灣時間下午3點45分,全球的數學家和數學迷們,都將目光聚焦於德國的海德堡桂冠論壇(Heidelberg Laureate Forum);世界各地的數學家和電腦科學家每年一度聚集於此,和獲邀的學界大師進行交流。演講台上,英國頂尖數學家麥可.阿蒂亞(Michael Atiyah)正準備發表黎曼猜想(Riemann hypothesis)的證明。
阿蒂亞無疑是第一流的數學家,獲獎無數,包括數學界的最高榮譽──費爾茲獎(Fields Medal)和阿貝爾獎(Abel Prize)。1929年出生、89歲高齡的他,於數天前宣佈,用「基進的新途徑」(radically new approach)解決了困擾數學家達 159年的黎曼猜想,並會在海德堡桂冠論壇發表。
Is Sir Michael Atiyah giving lecture on Monday Sept. 25 @ #HLF18? Yes.
Will he presenenting a proof of the Riemann Hypothesis? Yes, that is what his abstract says. pic.twitter.com/v1dJhUUUEk— Heidelberg Laureate Forum (@HLForum) 2018年9月20日
什麼是「黎曼猜想」?
1859年,德國數學家黎曼(Georg Friedrich Bernhard Riemann,1826-1866)在他的論文〈論小於給定數值的質數數目〉中,首次提及這個猜想。

德國數學家黎曼(Georg Friedrich Bernhard Riemann)source:Wikimedia
如我們國中所學,像2、3、5、7、11、13…等等,這些除了 1 跟自己本身以外,不能被其他正整數整除的數,稱為質數;而所有大於1的正整數,都能夠以質數的乘積來表示,例如 66=11×3×2。質數的概念很簡單,但是,如果我們問:「比某個特定數值要小的質數有多少個呢?質數在整個數列中的分布情況又是如何?」那就不是容易的問題、甚至是讓數學家們頭痛不已的問題。
黎曼在該篇論文中發現,質數的分布跟某個函數有著密切關係──該函數現被稱為黎曼ζ函數(Riemann zeta function);它的長相如下:
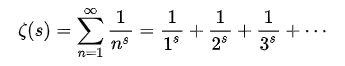
這看起來並不嚇人,起碼跟國中學過的無窮級數並沒有太大差別。上述式子裡,s是複數,可以寫成s=a+bi這樣的形式;a稱為s的實部、b是s的虛部、i則是根號負一。數學家們可以輕易證明,只要 s的實部大於1,那麼整個無窮級數裡,把每一項的絕對值相加後,會得到收斂並趨近於某個定值的結果。
不過,對於s的實部小於1的狀況,事情就沒那麼簡單了:整個級數和可能會發散──但是我們又想要擴充函數的定義,讓它適用更廣泛的範圍,那該怎麼辦呢?
運用一些數學技巧(很恐怖,不要問),針對s的實部小於1的狀況,可以將黎曼ζ函數表示為
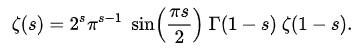
當中的 Г 稱為伽瑪函數(gamma function)。藉由這個新的定義,我們發現,當s為負偶數(s= -2, -4, -6…)時,黎曼ζ函數為零──這些s的值,我們稱為平凡零點。
但是,除了平凡零點之外,還有其他一些s的值,能夠讓黎曼ζ函數為零──稱為非平凡零點;它們不但對質數的分布有著決定性影響,實數部份還全都位於零和一之間。針對這一點,雖然黎曼本人無法證明,但他進一步猜測這些非平凡零點有著共同的特性:
黎曼ζ函數所有非平凡零點的實部都是二分之一
這就是赫赫有名的黎曼猜想。沒想到,這一猜想從 1859年被提出,至今已 159年,期間有數不清的數學家向其挑戰,卻無人能給出信服的證明。
黎曼猜想真的這麼難證明嗎?為何它讓數學家魂牽夢縈?
十九世紀末至二十世紀初最重要的數學家之一希爾伯特(David Hilbert,1862-1943),於1900年提出了23個他認為最重要的數學問題(其中有好些對二十世紀的數學發展起了莫大影響),當中就包含黎曼猜想。他曾表示:「如果我能在沉睡一千年後醒來,我的第一個問題將會是:『黎曼猜想被證明了嗎?』」
無獨有偶,一百年後,美國克雷數學研究所[1](Clay Mathematics Institute, CMI)選了當今數學界的七大問題(稱為「千禧年大獎難題(Millennium Prize Problems)」),並懸賞一百萬美金,給予能解決任何一個問題的數學家──其中也包含了黎曼猜想。事實上,黎曼猜想是唯一同時列於希爾伯特和克雷數學研究所名單上的問題,屹立不搖地等待數學家挑戰。
因為黎曼猜想與質數分布具有密切的關係,一旦被證明,數學家們將對質數的分布位置有更確切的認知,此無疑是數論(number theory)這一數學分支的重要突破。不僅如此,黎曼ζ函數的非平凡零點,也被發現跟某些物理系統具有相似的分布規律,至今無人能給出滿意的解釋。再者,數學文獻裡,許多數學命題都以黎曼猜想或其推廣的成立為前提;換言之,如果黎曼猜想(及其推廣)被證明,這些基於黎曼猜想的數學命題便能被一舉確認為真──可謂一人得道,雞犬升天。這樣的數學命題粗略估計至少有上千條。毋怪乎,有些數學家將黎曼猜想的證明形容為「數學的聖杯」。

有些數學家將黎曼猜想的證明形容為「數學的聖杯」,還好得到這個聖杯不用打聖杯戰爭(誤),卻也不是那麼容易。source:CucombreLibre @Flickr
黎曼猜想研究於歷史上的進展
在解決黎曼猜想這個終極對手的旅途中,人類是否曾碰上一些小頭目,得以賺取經驗值升級呢?
答案是肯定的。
如同角色扮演遊戲(role-playing video game, RPG)裡,我們大致可將攻擊手段區分為遠距攻擊和近距攻擊兩種,數學家在面對黎曼猜想這個強敵時,也主要從兩方面來著手。

數學家在面對黎曼猜想這個強敵時,就像在RPG遊戲裡我們從遠距和近距離攻擊同時著手。source:BagoGames @Flicr
一是去實際計算非平凡零點的數值,看看它們的實數部份是否符合黎曼猜想的二分之一;雖然這樣做並無法窮舉所有(也就是無限多)的非平凡零點,而證明黎曼猜想,卻能間接增強我們對黎曼猜想的信心──運氣好找到反例的話,更能一舉否證黎曼猜想。第二種方式則是直接對黎曼ζ函數下手,利用解析的方式證明黎曼猜想。
在非平凡零點的數值計算上,雖然黎曼自己有算過,卻並沒有發表;到1903年,才終於有數學家給出15個非平凡零點的數值──它們的實部都是二分之一。1932年,西格爾(Carl Ludwig Siegel,1896-1981)從已去世的黎曼的手稿中,挖掘出黎曼計算非平凡零點的方法,大舉推進了此一方向的研究。到了二十世紀中期,因為電腦的發明,計算零點的工作突飛猛進,有一萬個以上的非平凡零點都被確認實部為二分之一。至2004年,憑藉著更嶄新的計算法,已經有10000000000000(十萬億)個非平凡零點被確認符合黎曼猜想,而且沒有任何反例。
另一方面,也有人利用解析的方式嘗試證明黎曼猜想。1896年,兩位數學家分別獨立證明了,在複數平面、實數為一的線上沒有零點;換言之,非平凡零點的實部絕不可能為一。1914年,數學家哈代(Godfrey Harold Hardy,1877-1947)發現,在實數為二分之一的線上,有無限個非平凡零點──即使如此,這並無法保證「所有」非平凡零點的實部均為二分之一;更糟的是,根據哈代和李特爾伍德[2](John Edensor Littlewood,1885-1977)於1921年的估計,這些實部為二分之一的非平凡零點,只佔了全部非平凡零點的一小部份比例,趨近於零。
關於上述比例的研究,在1942年,才被塞爾伯格(Atle Selberg,1917-2007)證明其大於零;到了近期的2011年,這個數字被數學家推進到 41.05%──當然,距離 100%還很遠……
就在黎曼猜想的證明似乎還遙不可及的現今,事情突然有了戲劇性的變化:當代最出名、也最重要的數學家之一,麥可.阿蒂亞,將於本屆的海德堡桂冠論壇發表他對黎曼猜想的證明!
這次的黎曼猜想證明值得期待嗎?
就如同網路上一堆神人自稱推翻了相對論跟量子力學一樣,也有數不清的人,包括數學家,宣稱證明了黎曼猜想;然而,到目前為止,並沒有任何讓學界信服的說法。
這次宣佈證明了黎曼猜想的阿蒂亞,是第一流的數學家,所以確實讓不少人引頸期盼他的成果;只不過,因著阿蒂亞的89歲高齡,也讓一些人懷疑他是否真能提出說服所有人的證明。
無論如何,隨著在海德堡桂冠論壇的發表,數學家們將忙碌好一段時間,仔細檢視阿蒂亞的證明是否存有任何漏洞。最終結論,要之後才會知道了。
具有「數學王子」美譽的數學家高斯(Johann Carl Friedrich Gauss,1777-1855)曾表示:「數學是科學的皇后──而數論是數學的皇后」。黎曼猜想作為數論領域最重要的猜想、數學的聖杯,一旦被證明,將會是二十一世紀最重要的科學成就之一──讓我們拭目以待!
參考資料
- E. Bombieri (2000), Problems of the Millennium: the Riemann Hypothesis, Clay Mathematics Institute.
- D. Allen, K. Bonetta-Martin, E. Codling and S. Jefferies, The Riemann Hypothesis, The Plymouth Student Scientist, 2016, 9, (2), 249-257.
- Riemann hypothesis, Wikipedia.
- 盧昌海(2015),《黎曼猜想漫談》,五南。
註釋
- [1] 克雷數學研究所是總部設在美國新罕布夏州的非營利私人機構;機構目的在於促進和傳播數學知識。
- [2] 如果讀者還有印象,2016年台灣上映了介紹數學家拉馬努金生平的電影《天才無限家》;拉馬努金在英國的恩人兼研究夥伴就是哈代和李特爾伍德。
The post 數學界的聖杯「黎曼猜想證明」,是否已被人類得手? appeared first on PanSci 泛科學.