過年期間，我讀了這本《幸運的科學》。「裡面有提到貝氏定理（數學）。」朋友跟我說的時候，我還有點存疑，畢竟這書名怎麼看都有點像是那種、打著科學招牌，講一些科學「目前」還幫不上忙的領域。
讓我決定翻開的原因是作者之一 Barnaby Marsh 曾是哈佛大學、牛津大學的訪問學者，如今正在普林斯頓高等研究院訪問。前兩間是知名的大學，普林斯頓高等研究院更是當年匯集了馮·諾伊曼、愛因斯坦、奧本海默等留名青史學者的研究機構。
能訪問這些赫赫有名大學研究機構的學者所說的話，應該還蠻值得一看的吧？我的偏見這樣告訴我。
說到底，偏見也可以用機率來解釋：
如果今天只是一般人講幸運的科學，我們以為穿鑿附會的機率很高；但如果有像作者這樣的經歷，我們就下意識的認為可信度高一些，這是條件機率教我們的。
沒想到我翻開書讀起來，還真的有貝氏定理！
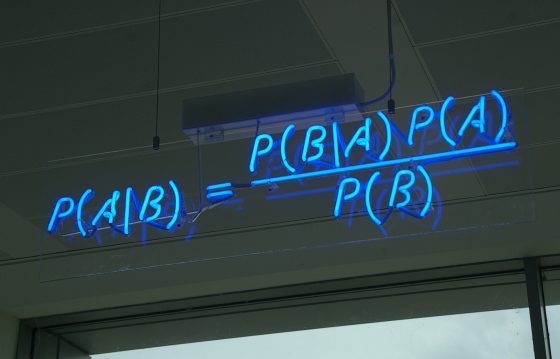
貝式定理。圖／Flickr
天助自助者，怎麼讓隨機事件成功機率增加？
格雷茨基在一九八〇年代與一九九〇年代先後四次奪得斯坦利盃 (Stanley Cup) 冠軍，創下至今無人能超越的得分紀錄。當他被問到如何打進這麼多球時，他永遠只有一個答案：「我滑到冰球會到的地方。」
這是一本有趣的書，作者用了兩三百頁的分量來解釋「天助自助者」、「趨吉避凶」這些我們自以為熟知，卻不太清楚該如何徹底落實在生活中的概念。其中有些重點精準的運用了「數學語言」來描述，讓讀者（至少我）更了解他想傳遞的概念。
比方說，成功或多或少都參雜了些機運，因此作者把成功定義為一個「隨機事件」。沒有人能控制隨機事件，無法讓隨機變成確定。
但透過兩件事，能讓成功更容易發生：
一、德蕾莎修女搭頭等艙事件 ── 增加成功機運
「以照顧貧苦病痛之人為己任的修女，竟然也有想要追求享受的一面，是想在旅途中舒服些嗎？」書中提到德雷莎修女搭頭等艙這行為受到一些批評。
你可以想像，這件事如果在台灣鐵定會上報紙頭條，然後被媒體公審。我自己查了網路資料，有一說是德雷莎修女在搭飛機時，常會被航空公司自動升級到頭等艙。但其實德雷莎修女是為了尋求更多的募款機會，精準一點的說，是「尋求更多遇到有錢人的機會」。
沒人能保證一次募款能否成功，但修女利用搭頭等艙來增加遇見富人的機率，進而提升募款次數。用個熟悉的數學例子來說，就是你無法改變丟硬幣出現正面的機率，但你可以多丟幾次。
只是生活中很多情境不像丟銅板那麼簡單，無法輕易的增加嘗試次數。有時候增加嘗試次數需要過高的成本，不一定值得去做，例如買彩券；或者，「嘗試增加次數」本身就是一個隨機事件，就像募款的例子。你沒辦法說「1 個富人沒用，那我就來遇 10 個富人吧！」。只是寫 10 封 E-mail 可能也只是徒勞的嘗試，因為這些信件通常都不會被認真看待，還是得要面對面的交流；搭頭等艙雖然不保證能遇到富人，但至少比起在便利商店遇到要來得機率高。
募款成功的機率不能被改變，但遇到富人的機率可以被改變，而這連帶會影響到募款成功的次數，所以這便是值得去做的一件事。
至於為什麼遇到富人的機率可以被改變，這就牽扯到書中的第二個重點 ── 條件機率。
二、嬰兒該不該和父母同床事件 ── 條件機率
我發現，即使是那些斷言一切都是命中注定、我們不可能改變的人，他們過馬路時仍然會注意兩邊來車。
圖／pixabay
書裡舉的例子是作者跟他太太在女兒出生時，曾經討論過要不要讓她跟她們一起睡。太太認為不妥，因為跟父母同睡的嬰兒發生意外的機率，是睡在嬰兒床上的 5 倍高，因為同床的嬰兒比較容易被悶住或被大人壓到 ── 但這是一般論的結果。
作者仔細研究後發現，許多意外是發生在父母喝醉、過度肥胖、教育程度不高的情況下（這邊作者沒有解釋清楚，但我想背後是指教育程度不高的父母，有相對高的比例會選擇不準備嬰兒床）；另外，床鋪過軟、沙發、水床、過多的毛毯也都是問題。
作者根據自己家裡的情況考量後，發現他們與女兒同床的風險是低於千分之一的。
換句話說，以下兩種機率是相差很多的：
- 嬰兒跟父母同床發生意外的機率。
- 給定 king size 床，且夫妻各用一條單人被的條件下，嬰兒跟父母同床發生意外的機率。
再用我們習慣的骰子做例子：丟骰子出現六點的機率是 1/6，但相信很多人小時候（或現在依然是）丟骰子時，會刻意把六點的那一面朝上或朝下，因為我們不知怎麼地，以為這樣比較容易出現六點 ── 這就是試圖以增加條件，把機率變成條件機率，進而趨吉避凶。不過六點這面朝上，這個方法事實上可能沒什麼效就是了。
我們會刻意把六點的那一面朝上或朝下，試圖把機率變成條件機率，不過這個方法事實上可能沒什麼效。
圖／pixabay
說說其他例子：以前有一位老師跟我說：「大家都說：『創業成功的機率只有 5%，所以創業很難。』這是錯的。舉個極端一點的例子：可能是有 99% 的人缺乏某些特質，注定失敗，有 1% 的人怎麼創業都成功。重點不在成功的機率，而在於你有沒有具備哪些條件。」
平均的機率或統計有一定的代表意義，但在套到自己身上時都必須根據自身的條件重新去思考。反過來說，我們可以不斷增加各種條件，讓自己想實現的事件，變成機率值越來越高的條件機率。
作者對此有一個很漂亮的說法：有一個打敗機率的方法，就是將它們個人化。
再回到前面過馬路的例子來說，被車撞到是隨機事件，而過馬路前先左右張望，不也就是再增加條件，把它變成條件機率嗎？
要如何更幸運？
這本書有好幾個段落當讓我覺得很有趣：早就學過的機率知識，許多正面思考的書籍中常見的情境與道理，串在一起後卻讓人有種「原來還能從這個角度看啊」的新奇感，就好像看見老朋友不曾見過的那面一樣。
從這樣實用面來介紹條件機率，也比「給定出現的點數是奇數，求出現 3 點的機率是多少？」這樣的題目，更讓人有感、覺得數學好玩有用 …… 說到最後有點離題了。
本書的主旨是講如何更幸運，範圍非常廣泛，從工作、愛情、到育兒都講了。雖然這不是我的專長，但裡面的一些觀點卻讓我覺得有趣，或許也會放在心上，想找機會用用看（像是我個人很喜歡教養那邊，作者認為孩子需要的是「能辨認他們眼前所有可能導致快樂的途徑的能力」），雖然這都只是很個人主觀的看法而已。
不過如果對機率有興趣，想看看專家怎麼把機率與幸運做結合，相信書中前面的幾章，你應該會讀得蠻開心的。
圖／pixabay
The post 用我大數學的語言傳授幸運法則！？ ── 《幸運的科學》書評 appeared first on PanSci 泛科學.